Deep neural networks have enabled technological wonders starting from voice recognition to machine transition to protein engineering, however their design and utility is nonetheless notoriously unprincipled.
The event of instruments and strategies to information this course of is without doubt one of the grand challenges of deep studying principle.
In Reverse Engineering the Neural Tangent Kernel, we suggest a paradigm for bringing some precept to the artwork of structure design utilizing latest theoretical breakthroughs: first design kernel operate – typically a a lot simpler job – after which “reverse-engineer” a net-kernel equivalence to translate the chosen kernel right into a neural community.
Our predominant theoretical end result allows the design of activation features from first rules, and we use it to create one activation operate that mimics deep (textrm{ReLU}) community efficiency with only one hidden layer and one other that soundly outperforms deep (textrm{ReLU}) networks on an artificial job.

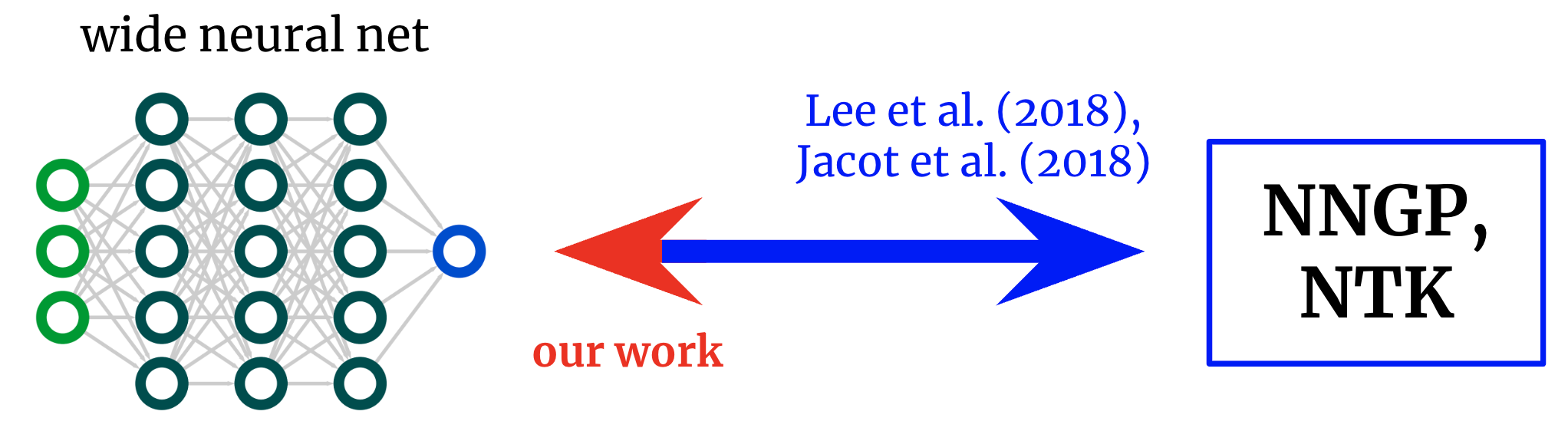
Kernels again to networks. Foundational works derived formulae that map from broad neural networks to their corresponding kernels. We receive an inverse mapping, allowing us to start out from a desired kernel and switch it again right into a community structure.

Neural community kernels

The sector of deep studying principle has not too long ago been remodeled by the conclusion that deep neural networks typically turn out to be analytically tractable to check within the infinite-width restrict.
Take the restrict a sure approach, and the community the truth is converges to an strange kernel methodology utilizing both the structure’s “neural tangent kernel” (NTK) or, if solely the final layer is skilled (a la random characteristic fashions), its “neural community Gaussian course of” (NNGP) kernel.
Just like the central restrict theorem, these wide-network limits are sometimes surprisingly good approximations even removed from infinite width (typically holding true at widths within the a whole lot or hundreds), giving a outstanding analytical deal with on the mysteries of deep studying.

From networks to kernels and again once more

The unique works exploring this net-kernel correspondence gave formulae for going from structure to kernel: given an outline of an structure (e.g. depth and activation operate), they provide the community’s two kernels.
This has allowed nice insights into the optimization and generalization of assorted architectures of curiosity.
Nevertheless, if our objective will not be merely to grasp current architectures however to design new ones, then we would quite have the mapping within the reverse route: given a kernel we would like, can we discover an structure that provides it to us?
On this work, we derive this inverse mapping for fully-connected networks (FCNs), permitting us to design easy networks in a principled method by (a) positing a desired kernel and (b) designing an activation operate that provides it.

To see why this is smart, let’s first visualize an NTK.
Contemplate a large FCN’s NTK (Okay(x_1,x_2)) on two enter vectors (x_1) and (x_2) (which we’ll for simplicity assume are normalized to the identical size).
For a FCN, this kernel is rotation-invariant within the sense that (Okay(x_1,x_2) = Okay(c)), the place (c) is the cosine of the angle between the inputs.
Since (Okay(c)) is a scalar operate of a scalar argument, we are able to merely plot it.
Fig. 2 reveals the NTK of a four-hidden-layer (4HL) (textrm{ReLU}) FCN.

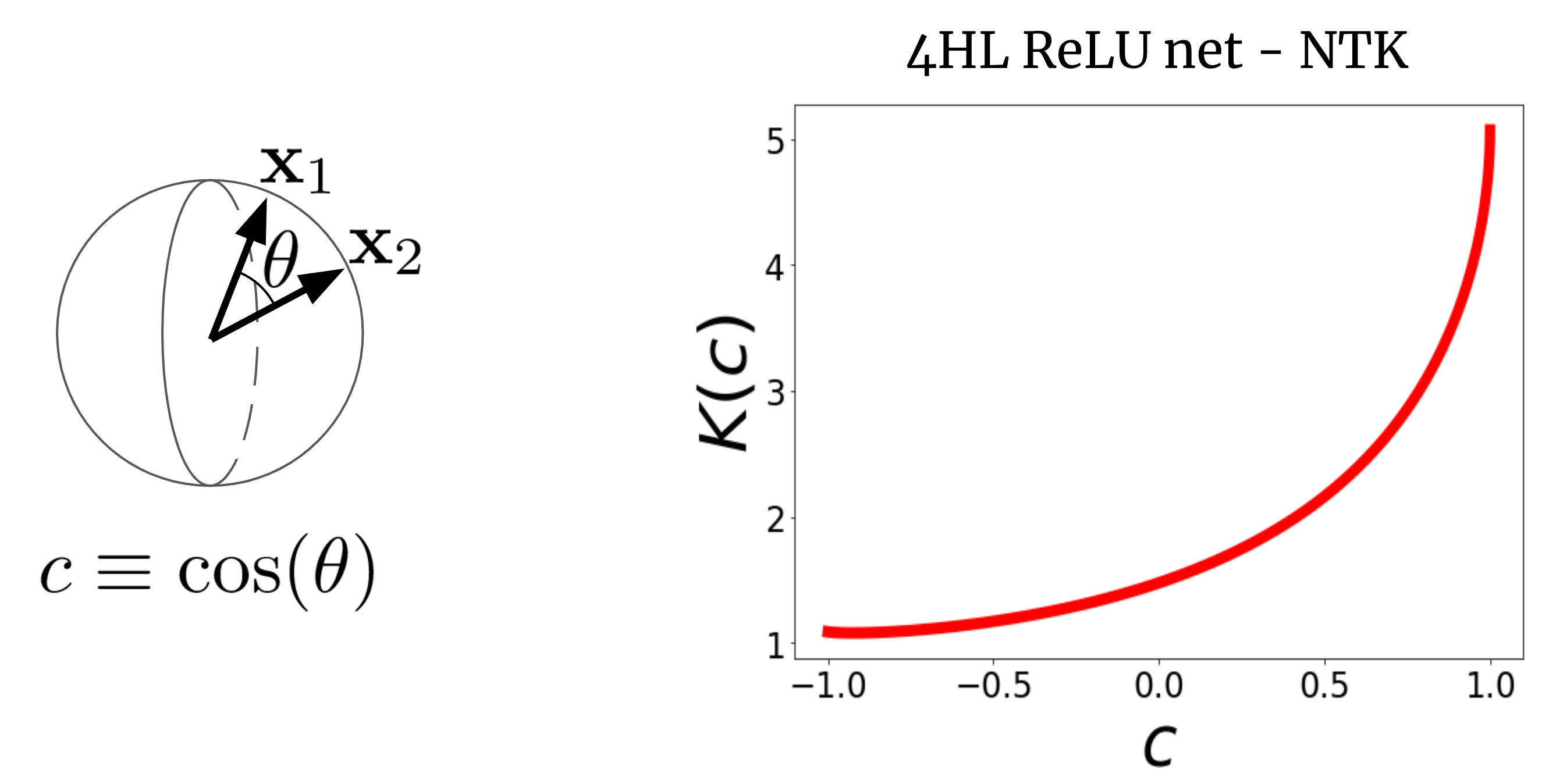
Fig 2. The NTK of a 4HL $textrm{ReLU}$ FCN as a operate of the cosine between two enter vectors $x_1$ and $x_2$.

This plot truly incorporates a lot details about the training conduct of the corresponding broad community!
The monotonic improve implies that this kernel expects nearer factors to have extra correlated operate values.
The steep improve on the finish tells us that the correlation size will not be too giant, and it could match sophisticated features.
The diverging by-product at (c=1) tells us concerning the smoothness of the operate we count on to get.
Importantly, none of those info are obvious from a plot of (textrm{ReLU}(z))!
We declare that, if we need to perceive the impact of selecting an activation operate (phi), then the ensuing NTK is definitely extra informative than (phi) itself.
It thus maybe is smart to attempt to design architectures in “kernel house,” then translate them to the standard hyperparameters.

An activation operate for each kernel

Our predominant result’s a “reverse engineering theorem” that states the next:

Thm 1: For any kernel $Okay(c)$, we are able to assemble an activation operate $tilde{phi}$ such that, when inserted right into a single-hidden-layer FCN, its infinite-width NTK or NNGP kernel is $Okay(c)$.

We give an express method for (tilde{phi}) by way of Hermite polynomials
(although we use a special purposeful type in follow for trainability causes).
Our proposed use of this result’s that, in issues with some recognized construction, it’ll typically be potential to put in writing down kernel and reverse-engineer it right into a trainable community with numerous benefits over pure kernel regression, like computational effectivity and the power to be taught options.
As a proof of idea, we check this concept out on the artificial parity drawback (i.e., given a bitstring, is the sum odd and even?), instantly producing an activation operate that dramatically outperforms (textual content{ReLU}) on the duty.

One hidden layer is all you want?

Right here’s one other stunning use of our end result.
The kernel curve above is for a 4HL (textrm{ReLU}) FCN, however I claimed that we are able to obtain any kernel, together with that one, with only one hidden layer.
This means we are able to give you some new activation operate (tilde{phi}) that provides this “deep” NTK in a shallow community!
Fig. 3 illustrates this experiment.

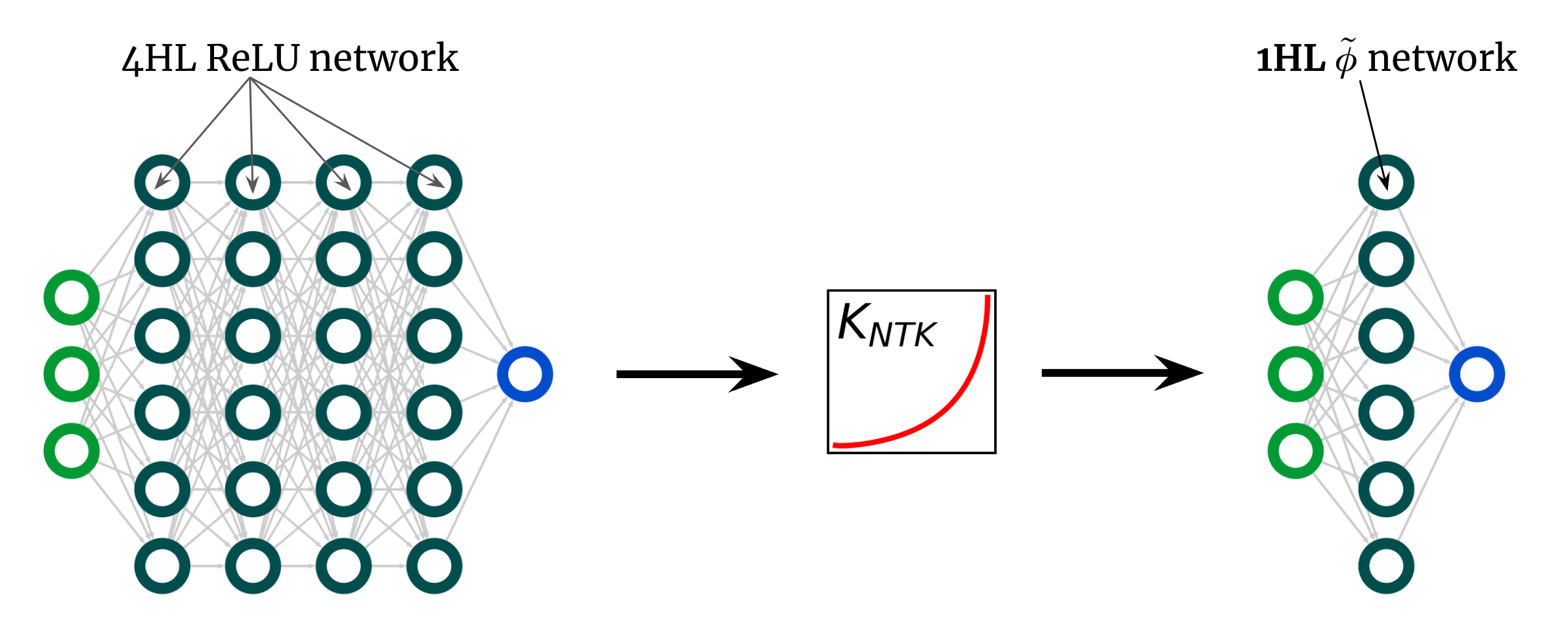
Fig 3. Shallowification of a deep $textrm{ReLU}$ FCN right into a 1HL FCN with an engineered activation operate $tilde{phi}$.

Surprisingly, this “shallowfication” truly works.
The left subplot of Fig. 4 beneath reveals a “mimic” activation operate (tilde{phi}) that provides nearly the identical NTK as a deep (textrm{ReLU}) FCN.
The appropriate plots then present prepare + check loss + accuracy traces for 3 FCNs on a typical tabular drawback from the UCI dataset.
Notice that, whereas the shallow and deep ReLU networks have very totally different behaviors, our engineered shallow mimic community tracks the deep community virtually precisely!

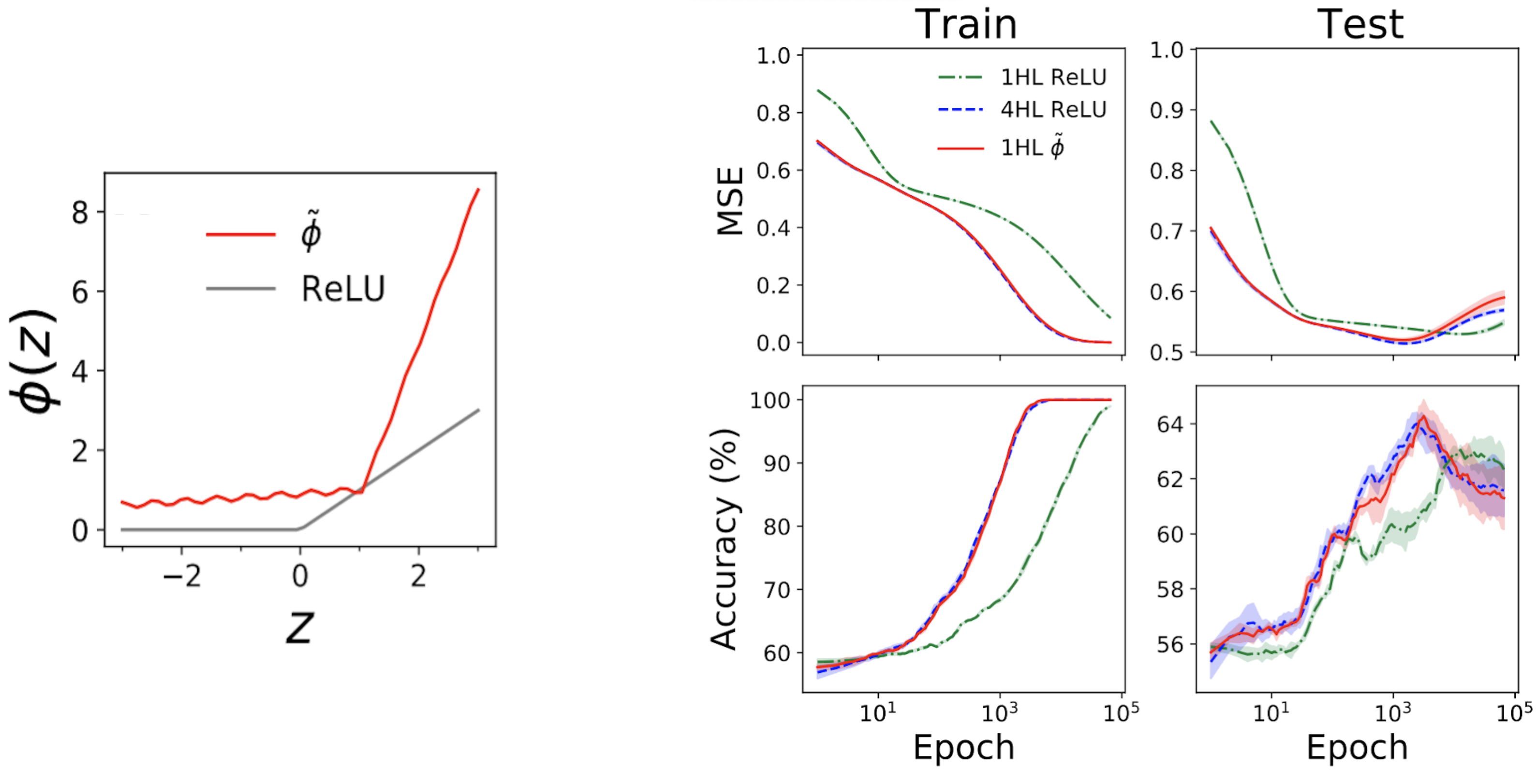
Fig 4. Left panel: our engineered “mimic” activation operate, plotted with ReLU for comparability. Proper panels: efficiency traces for 1HL ReLU, 4HL ReLU, and 1HL mimic FCNs skilled on a UCI dataset. Notice the shut match between the 4HL ReLU and 1HL mimic networks.

That is attention-grabbing from an engineering perspective as a result of the shallow community makes use of fewer parameters than the deep community to attain the identical efficiency.
It’s additionally attention-grabbing from a theoretical perspective as a result of it raises basic questions concerning the worth of depth.
A standard perception deep studying perception is that deeper will not be solely higher however qualitatively totally different: that deep networks will effectively be taught features that shallow networks merely can not.
Our shallowification end result means that, a minimum of for FCNs, this isn’t true: if we all know what we’re doing, then depth doesn’t purchase us something.

Conclusion

This work comes with numerous caveats.
The most important is that our end result solely applies to FCNs, which alone are not often state-of-the-art.
Nevertheless, work on convolutional NTKs is quick progressing, and we imagine this paradigm of designing networks by designing kernels is ripe for extension in some type to those structured architectures.

Theoretical work has thus far furnished comparatively few instruments for sensible deep studying theorists.
We intention for this to be a modest step in that route.
Even and not using a science to information their design, neural networks have already enabled wonders.
Simply think about what we’ll have the ability to do with them as soon as we lastly have one.

This submit relies on the paper “Reverse Engineering the Neural Tangent Kernel,” which is joint work with Sajant Anand and Mike DeWeese. We offer code to breed all our outcomes. We’d be delighted to discipline your questions or feedback.